实验题目:表达式求值
一、问题描述
设计一个中缀表达式求值的程序。此中缀表达式中涉及到的运算符有:(、)、+(加)、-(减)、*(乘)、/(除)、%(取余)、^(求幂)。程序需要处理这段中缀表达式的输入,并且判断表达式的正确性;如果表达式正确,则输出表达式的值;如果表达式非法,则输出规定的错误信息。并且,此中缀表达式中涉及到的操作数运算均为double浮点类型相关的运算。
关于输入与输出的要求:输入为中缀表达式,每个表达式占一整行;输出在表达式正确时为表达式求值的结果(精确到小数点后两位),在表达式错误时输出”ERROR IN INFIX NOTATION”这个错误提示信息。
二、算法描述
2.1 概述
表达式一般来说有三种:前缀表达式、中缀表达式、后缀表达式,其中后缀表达式又叫做逆波兰表达式。中缀表达式是最符合人们思维方式的一种表达式,顾名思义,就是操作符在操作数的中间。而前缀表达式和后缀表达式中操作符分别在操作数的前面和操作数的后面。
针对本实验的问题,会有两个解决的方案。第一种是,先将中缀表达式转换为后缀表达式,然后进行后缀表达式求值计算;第二种是,直接进行中缀表达式的求值计算。那么,中缀表达式和后缀表达式之间的区别是什么呢?两者的区别在于,中缀表达式更加符合人类的思维模式,不过需要括号进行辅助表达;而后缀表达式不需要括号就可以展现出哪部分的运算先进行,不需要去考虑优先级的问题,因此后缀表达方式恰好更加符合计算机的处理机制,对于计算机来说处理起来更加方便简单。在本次实验中,最后进行代码实现的算法是直接中缀表达式的求值计算。
2.2 中缀表达式求值
2.2.1 文字描述
对于中缀表达式求值来说,最直接的方式是使用两个栈,一个存放操作符,另一个存
放操作数。所以在处理中缀表达式字符串的时候,算法可以把需要处理的类型分为操作数类型和操作符类型。当遇到操作数的时候,直接把其压入存放操作数的栈中。操作符可以被分为三种情形去处理:当遇到的操作符为 ‘(‘ (左括号)时,直接将其压入存放操作符的栈中;当遇到的操作符为 ‘)’ (右括号)时,存放操作符的栈反复出栈计算,直到遇到左括号为止;当遇到的操作符为其他的时,讲此刻的操作符与栈顶的进行比较,若此刻的操作符优先级更高,则压入栈中,若优先级更低,则反复出栈计算直到栈顶操作符优先级小于此刻的操作符或栈为空后,将其压入栈中。
当处理完中缀表达式字符串中,如果操作符栈不为空,则将其中剩余的操作符配合操作数栈尽数弹出并且进行计算,直到操作符栈为空,操作数栈只有一个计算结果元素。此时,将结果输出即程序成功运行。
2.2.2 表达式错误检测
对于中缀表达式求值算法而言,还有两个细节点需要处理。第一个是负号的问题,由于负号和减号在表示上相同,本算法实现中使用 ‘#’ 字符去替换负号的原本的 ‘-’ 字符来进行处理。由算式的计算规则可知,只有当 ‘-’ 字符在 ‘)’ 左括号和数字的右侧时,才表示为减号,其余的地方都表示为负号。解决方式为,在进行计算之前,先对表达式字符串进行处理,筛选出负号字符,并将其转换为 ‘#’ 字符。
第二个是中缀表达式错误判定问题。会产生错误表达式的情况有:非法字符;括号不匹配;运算符不匹配。非法字符,即在中缀表达式字符串中出现了不被允许的字符;解决方式为,在计算之前的处理中加入规则逻辑进行判定。括号不匹配和运算符不匹配的判定方式为,程序最后是否出现多个操作数在栈中,或者操作数不够用,或者操作数和操作符不匹配的情况。解决方式为,在算法设计的类中规定一个布尔变量,当错误表达式被检测出来的时候,更新变量的值,并且在主程序中设定判定语句,及时检测出来,并输出错误信息然后退出程序。
2.2.3 核心代码实现原理
针对两个栈的需求,在算法中采用C++的STL中vector类型来模拟栈的操作;push_back作为压栈方法,pop_back作为出栈方法,back作为查看栈顶元素方法。对于表达式中单个子式的计算,采用Switch语句判断不同的运算符进行计算。另外,通过一个map类型常量来帮助算法判定运算符的优先级。
2.2.3 流程图描述
遍历中缀表达式字符串的流程图展示:
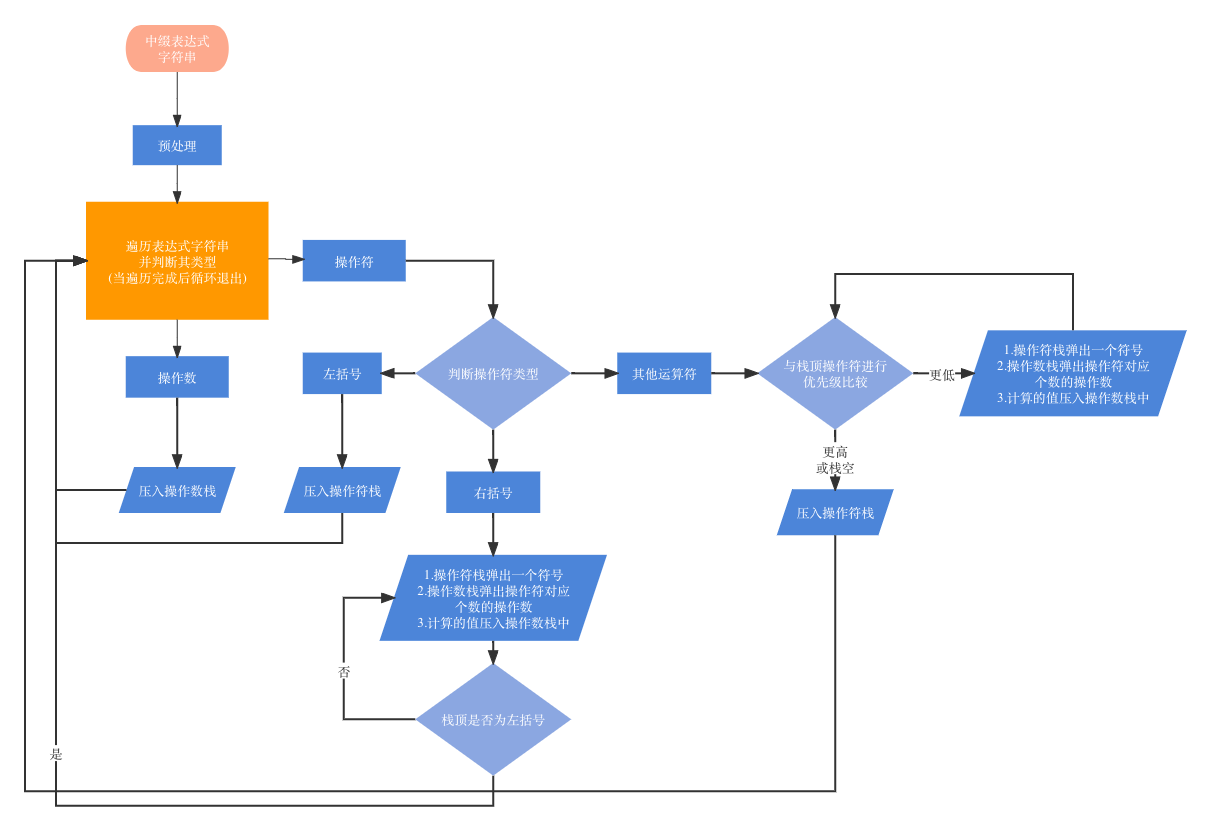
字符串遍历结束,处理后续剩下两个栈的流程图展示:
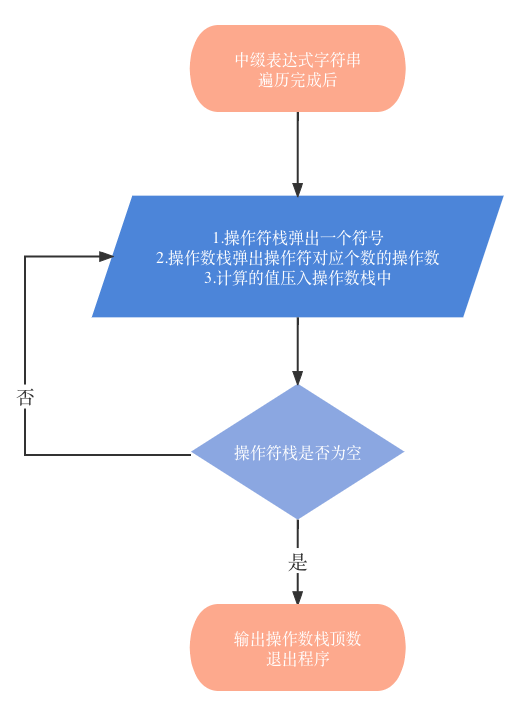
三、运行测试
| 测试编号 | 测试目的 | 输入 | 输出 | 正确性 |
|---|---|---|---|---|
| 1 | 括号不匹配检测 | 1+2( | ERROR IN INFIX NOTATION | ✅ |
| 2 | 括号不匹配检测 | 1+2()3 | ERROR IN INFIX NOTATION | ✅ |
| 3 | 括号不匹配检测 | 123*12+(12+63^2 | ERROR IN INFIX NOTATION | ✅ |
| 4 | 非法字符检测 | 6e3*9 | ERROR IN INFIX NOTATION | ✅ |
| 5 | 非法字符检测 | 6+(#3) | ERROR IN INFIX NOTATION | ✅ |
| 6 | 操作符错误检测 | 7+/89-35%10 | ERROR IN INFIX NOTATION | ✅ |
| 7 | 除0错误检测 | 1/0 | ERROR IN INFIX NOTATION | ✅ |
| 8 | 模0错误检测 | 1012%0 | ERROR IN INFIX NOTATION | ✅ |
| 9 | 复杂运算检测 | 2.5+(2^3/2)%3 | 3.50 | ✅ |
| 10 | 复杂运算检测 | 11/2%20 | 5.50 | ✅ |
| 11 | 复杂括号检测 | 3+5*(5+2+3*(5/5+2/(3-2)+5)%2)-2 | 36.00 | ✅ |
| 12 | 多乘方运算检测 | 2^2^3 | 256.00 | ✅ |
四、总结
实验测试的结果显示,本报告中的算法可以覆盖要求的所有运算符的运算,并且可以支持整数、小数的正确运算。从简单的表达式到复杂的多层次多嵌套的表达式,算法都能输出正确的结果。对于模运算不仅支持整型的运算,浮点数的运算功能也正确实现。同时,对于中缀表达式错误检测而言,在括号匹配检测、非法字符检测、操作符错误检测中都表现优秀,能够得到正确的结果;并且,对于除0和摸0错误计算的检测功能也得以实现。由此可以得出结论,该算法对于中缀表达式求值可以计算出正确的结果,对表达式的各种错误情况也可以正确判定;另外,该算法没有使用两层以上的循环逻辑,减少不必要的内存开销,时空复杂度的表现也非常可观。
附录:源代码