Intentional practicing is of great importance.
Definition
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
404. Sum of Left Leaves
Url: https://leetcode-cn.com/problems/sum-of-left-leaves/
Description: Given therootof a binary tree, return the sum of all left leaves.
# Author: eclipse
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
int sum = 0;
if (!root) return 0;
if (root->left && !root->left->left && !root->left->right) sum = root->left->val;
return sum + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
}
};
655. Print Binary Tree
Url: https://leetcode-cn.com/problems/print-binary-tree/
Description: Given the root of a binary tree, construct a 0-indexed m x n string matrix res that represents a formatted layout of the tree, a matrix layout. The matrix's row number isheight+1, while its column number is2^height-1.
# Author: eclipse
class Solution {
public:
vector<vector<string>> printTree(TreeNode* root) {
int h = getHeight(root);
int w = (1 << h) - 1;
vector<vector<string>> res(h, vector<string>(w, ""));
fillVec(root, res, 0, 0, w-1);
return res;
}
private:
int getHeight(TreeNode* root) {
if (!root) return 0;
return max(getHeight(root->left), getHeight(root->right)) + 1;
}
void fillVec(TreeNode *root, vector<vector<string>> &res, int h, int l, int r) {
if (!root) return;
int mid = (l + r) / 2;
res[h][mid] = std::to_string(root->val);
fillVec(root->left, res, h+1, l, mid-1);
fillVec(root->right, res, h+1, mid+1, r);
}
};
637. Average of Levels in Binary Tree
Url: https://leetcode-cn.com/problems/average-of-levels-in-binary-tree/
Description: Given the root of a binary tree, return the average value of the nodes on each level in the form of an array.
Solv1: DFS
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
if (root == nullptr) return {};
vector<double> ans;
vector<pair<long long, int>> sum_count;
// Count each level's sum of values.
preOrder(root, 0, sum_count);
// When sum_count is all set.
for (const auto& p : sum_count)
ans.push_back(static_cast<double>(p.first) / p.second);
return ans;
}
private:
void preOrder(TreeNode* root, int depth, vector<pair<long long, int>>& sum_count) {
if (root == nullptr) return;
if (depth >= sum_count.size()) sum_count.push_back({0,0});
sum_count[depth].first += root->val;
sum_count[depth].second++;
preOrder(root->left, depth+1, sum_count);
preOrder(root->right, depth+1, sum_count);
}
};
Solv2: BFS
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
if (root == nullptr) return {};
vector<double> ans;
vector<TreeNode*> curr, next;
curr.push_back(root);
// Process every level's nodes one by one.
while (!curr.empty()) {
long long sum = 0;
for (const auto& node : curr) {
sum += node->val;
if (node->left) next.push_back(node->left);
if (node->right) next.push_back(node->right);
}
ans.push_back(static_cast<double>(sum) / curr.size());
next.swap(curr);
next.clear();
}
return ans;
}
};
617. Merge Two Binary Trees
Url: https://leetcode-cn.com/problems/merge-two-binary-trees/
Description: Given two binary treesroot1 root2. Merge them together with requirements like: if overlapping, sum two nodes; Otherwise, the not null node will be used as the node of the new tree.
Solv1: modifying the original trees is not allowed
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if (root1 == nullptr) return root2;
if (root2 == nullptr) return root1;
auto root = new TreeNode(root1->val + root2->val);
root->left = mergeTrees(root1->left, root2->left);
root->right = mergeTrees(root1->right, root2->right);
return root;
}
};
Solv2: modifying the original trees is allowed
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if (root1 == nullptr) return root2;
if (root2 == nullptr) return root1;
auto root = root1;
root->val += root2->val;
root->left = mergeTrees(root1->left, root2->left);
root->right = mergeTrees(root1->right, root2->right);
return root;
}
};
606. Construct String from Binary Tree
Url: https://leetcode-cn.com/problems/construct-string-from-binary-tree/
Description: Given the root of a binary tree, construct a string consists of parenthesis and integers from a binary tree with the preorder traversing way, and return it. Omit all the empty parenthesis pairs that do not affect the one-to-one mapping relationship between the string and the original binary tree.
class Solution {
public:
string tree2str(TreeNode* root) {
if (root == nullptr) return "";
const string s = std::to_string(root->val);
const string l = tree2str(root->left);
const string r = tree2str(root->right);
// Special case 0: s()() -> s
if (root->left == nullptr && root->right == nullptr) return s;
// Special case 1: s(l)() -> s(l)
if (root->right == nullptr) return s + "(" + l + ")";
// General case: s(l)(r)
return s + "(" + l + ")" + "(" + r + ")";
}
};
112. Path Sum
Url: https://leetcode-cn.com/problems/path-sum/
Description: Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == nullptr) return false;
if (root->left == nullptr && root->right == nullptr)
return root->val == targetSum;
int new_targetSum = targetSum - root->val;
return hasPathSum(root->left, new_targetSum) || hasPathSum(root->right, new_targetSum);
}
};
113. Path Sum II
Url: https://leetcode-cn.com/problems/path-sum-ii/
Description: Given the root of a binary tree and an integer targetSum, return all root-to-leaf paths where the sum of the node values in the path equals targetSum. Each path should be returned as a list of the node values, not node references. A root-to-leaf path is a path starting from the root and ending at any leaf node.
class Solution {
public:
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
vector<vector<int>> ans;
vector<int> curr;
pathSum(root, targetSum, curr, ans);
return ans;
}
private:
void pathSum(TreeNode* root, int targetSum, vector<int>& curr, vector<vector<int>>& ans) {
if (root == nullptr) return;
if (root->left == nullptr && root->right == nullptr) {
if (root->val == targetSum) {
ans.push_back(curr);
ans.back().push_back(root->val);
}
return;
}
curr.push_back(root->val);
int newTargetSum = targetSum - root->val;
pathSum(root->left, newTargetSum, curr, ans);
pathSum(root->right, newTargetSum, curr, ans);
curr.pop_back();
}
};
100. Same Tree
Url: https://leetcode-cn.com/problems/same-tree/
Description: Given the roots of two binary trees p and q, write a function to check if they are the same or not. Both structurally and node's value-side identical.
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
// Case 0: p and q are all empty.
if (p == nullptr && q == nullptr) return true;
// Case 1: p and q are not all empty.
if (p == nullptr || q == nullptr) return false;
// Case 2: p and q are not empty but values are not the same.
if (p->val != q->val) return false;
// Recursively compare left-subtree and right-subtree.
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
};
110. Balanced Binary Tree
Url: https://leetcode-cn.com/problems/balanced-binary-tree/
Description: Given a binary tree, determine if it is height-balanced.
The definition of Height-Balanced:
A binary tree in which the left and right subtrees of every node differ in height by no more than 1.
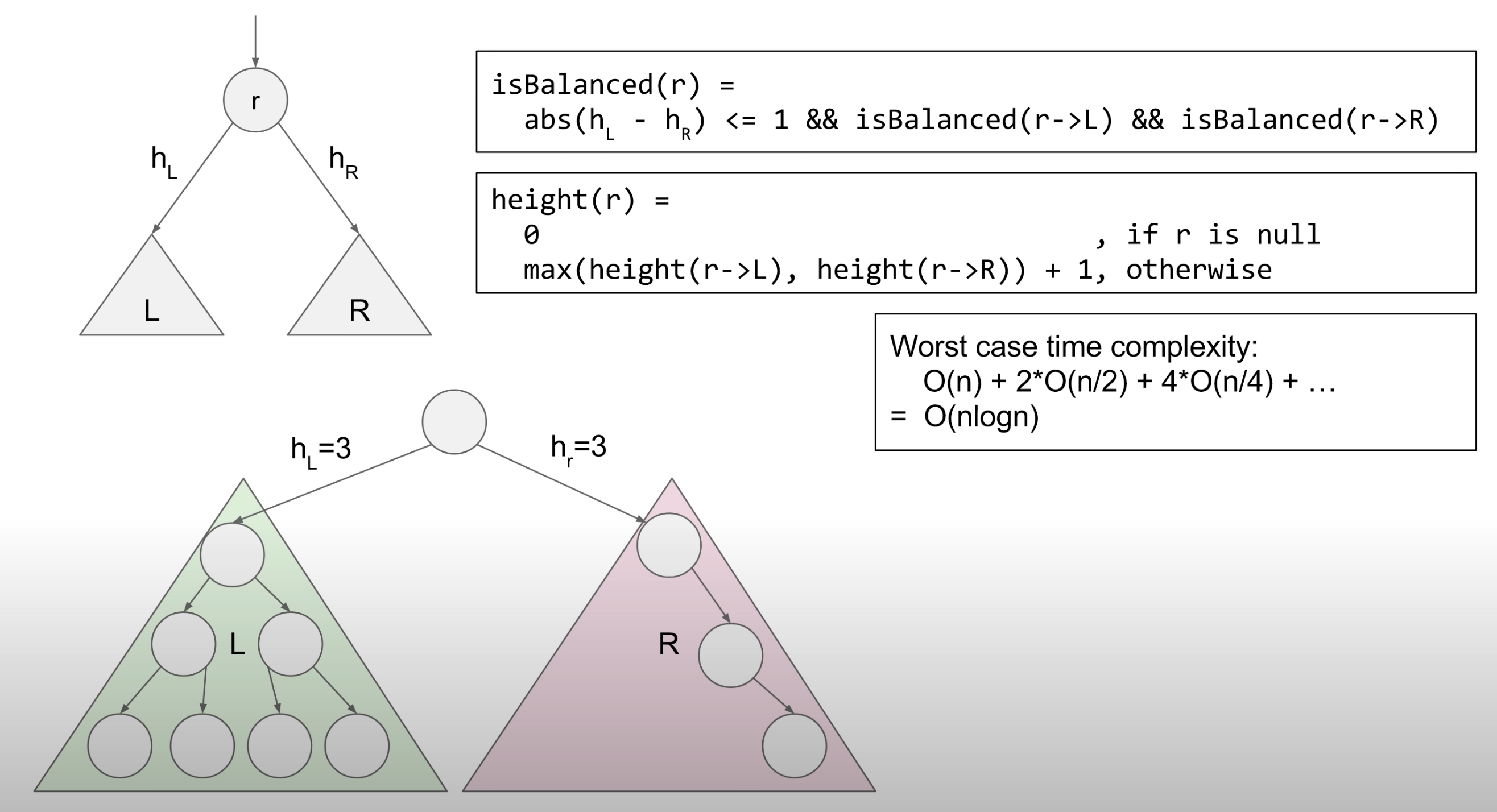
Solv1: recursively check isBalanced and calculate height. O(nlogn)
class Solution {
public:
bool isBalanced(TreeNode* root) {
if (root == nullptr) return true;
int leftHeight = getHeight(root->left);
int rightHeight = getHeight(root->right);
return (abs(leftHeight - rightHeight)<=1) && isBalanced(root->left) && isBalanced(root->right);
}
private:
int getHeight(TreeNode* root) {
if (root == nullptr) return 0;
return max(getHeight(root->left), getHeight(root->right)) + 1;
}
};
Solv2: recursively calculate height as well as checking isBalanced. O(n)
class Solution {
public:
bool isBalanced(TreeNode* root) {
if (root == nullptr) return true;
bool balanced = true;
check(root, balanced);
return balanced;
}
private:
int check(TreeNode* root, bool& balanced) {
if (root == nullptr) return 0;
int leftHeight = check(root->left, balanced);
int rightHeight = check(root->right, balanced);
if (abs(leftHeight - rightHeight) > 1) {
balanced = false;
return -1;
}
return max(leftHeight, rightHeight) + 1;
}
};
102. Binary Tree Level Order Traversal
URL: https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
Description: Given the root of a binary tree, return the level order traversal of its nodes' values.

class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
return BFS(root);
}
private:
vector<vector<int>> BFS(TreeNode* root) {
if (root == nullptr) return {};
vector<vector<int>> ans;
vector<TreeNode*> curr, next;
curr.push_back(root);
while (!curr.empty()) {
ans.push_back({});
for (const auto node : curr) {
ans.back().push_back(node->val);
if (node->left) next.push_back(node->left);
if (node->right) next.push_back(node->right);
}
next.swap(curr);
next.clear();
}
return ans;
}
};
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ans;
DFS(root, 0, ans);
return ans;
}
private:
void DFS(TreeNode* root, int depth, vector<vector<int>>& ans) {
if (root == nullptr) return;
// Suitable for pre/in/post order traversal.
while (ans.size() <= depth) ans.push_back({});
DFS(root->left, depth+1, ans);
DFS(root->right, depth+1, ans);
ans.at(depth).push_back(root->val);
}
};
671. Second Minimum Node In a Binary Tree
URL: https://leetcode-cn.com/problems/second-minimum-node-in-a-binary-tree/
Description: Given such a special binary tree, output the second minimum value in the set made of all the nodes' value in the whole tree. If no such second minimum value exists, output -1 instead.
Constraints:
1. non-empty special binary tree consisting of nodes with the non-negative value; 2. each node has 2 or 0 sub-node 3. root.val = min(root.left.val, root.right.val) 4. The number of nodes in the tree is in the range [1, 25] 5. 1 <= Node.val <= 231 - 1
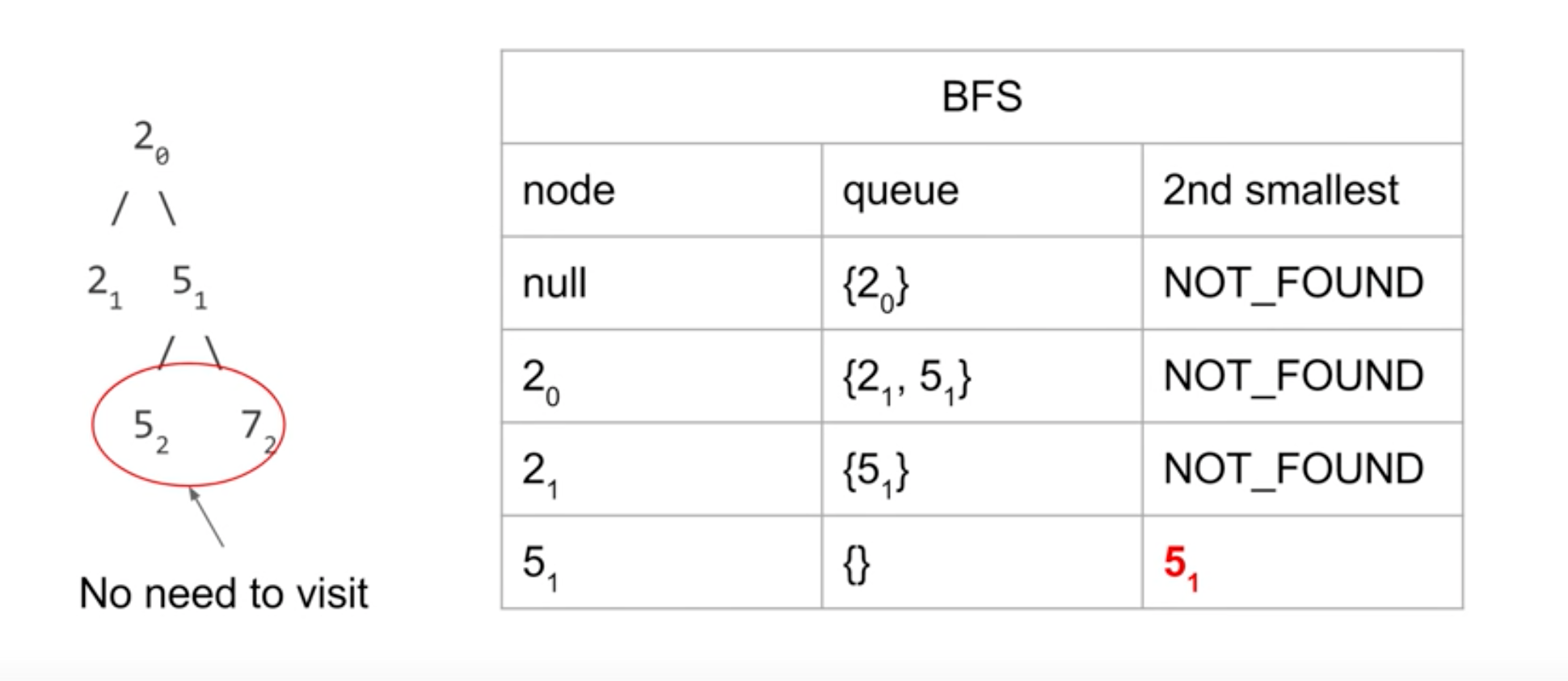
For the solution of BFS, the first time I use int s2 =INT_MAX to set s2, but one cause failed as submitting. The reason is that the biggest value available for node 2^31-1. The suitable initial value of s2 is INT32_MAX. Therefore, change to long long s2 = INT32_MAX and everything is all right.
class Solution {
public:
int findSecondMinimumValue(TreeNode* root) {
if (root == nullptr) return -1;
return BFS(root);
}
private:
int BFS(TreeNode* root) {
if (root == nullptr) return -1;
// Smallest value;
int s1 = root->val;
// Second small value;
long long s2 = INT32_MAX;
bool found = false;
deque<TreeNode*> q;
q.push_back(root);
while (!q.empty()) {
TreeNode* node = q.front();
q.pop_front();
// Keep update the second small value.
if (node->val > s1 && node->val <= s2) {
// If found a second small value under this queue,
// no need to add this node's children.
s2 = node->val;
found = true;
continue;
}
// If the second small value does not appear,
// keep adding this node's children into queue.
if (node->left == nullptr) continue;
q.push_back(node->left);
q.push_back(node->right);
}
return found ? s2 : -1;
}
};

class Solution {
public:
int findSecondMinimumValue(TreeNode* root) {
if (root == nullptr) return -1;
return DFS(root, root->val);
}
private:
// s1 is the current smallest value.
int DFS(TreeNode* root, int s1) {
if (root == nullptr) return -1;
// If root's value is already greater than s1,
// thus root's value is the second smallest one.
if (root->val > s1) return root->val;
// Otherwise, recursively seek root's children
// and check the smaller one.
int sl = DFS(root->left, s1);
int sr = DFS(root->right, s1);
if (sl == -1) return sr;
if (sr == -1) return sl;
return min(sl, sr);
}
};
669. Trim a Binary Search Tree
URL: https://leetcode-cn.com/problems/trim-a-binary-search-tree/
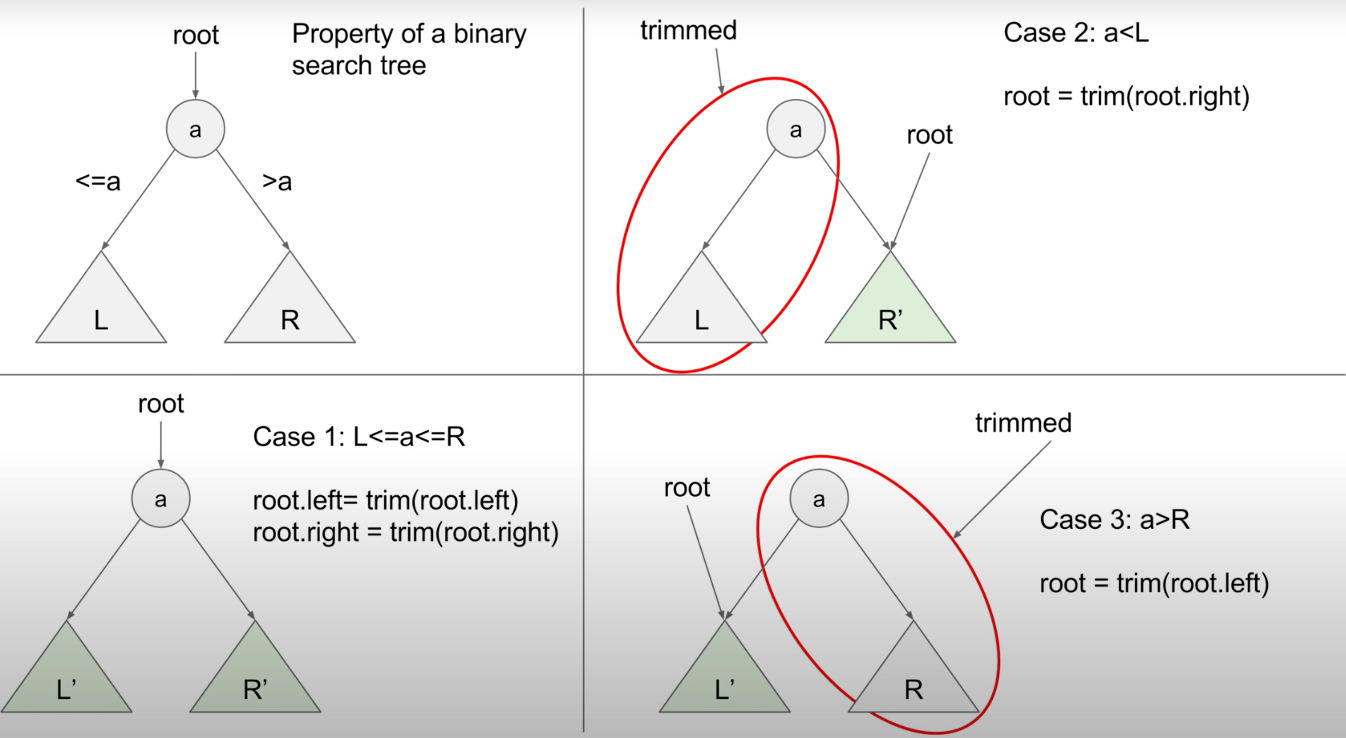
Description: Given the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a unique answer. Return the root of the trimmed binary search tree. Note that the root may change depending on the given bounds.
class Solution {
public:
// No cleanup means memory leak.
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr) return nullptr;
// If val not in range, return the left/right subtrees.
if (root->val < low) return trimBST(root->right, low, high);
if (root->val > high) return trimBST(root->left, low , high);
// If val in [low, high], recursively trim left/right subtrees.
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
};
654. Maximum Binary Tree
URL: https://leetcode-cn.com/problems/maximum-binary-tree/
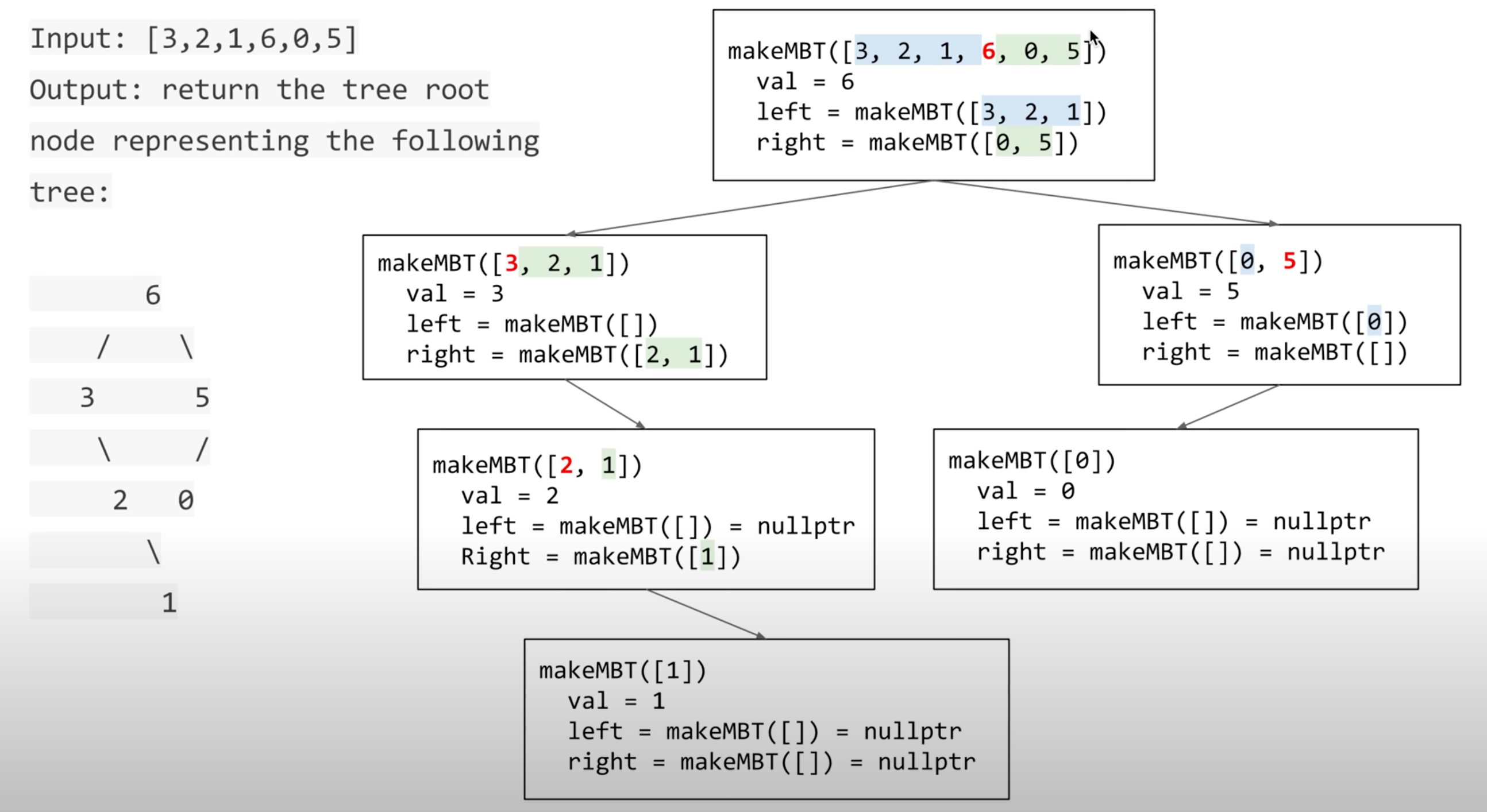
Description: You are given an integer array nums with no duplicates. Return a maximum binary tree built recursively from nums.Algorithm:
- Create a root node whose value is the maximum value in nums.
- Recursively build the left subtree on the subarray prefix to the left of the maximum value.
- Recursively build the right subtree on the subarray suffix to the right of the maximum value.
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
if (nums.empty()) return nullptr;
// Find the max element in nums -> O(n)
auto it = std::max_element(nums.begin(), nums.end());
TreeNode* root = new TreeNode(*it);
vector<int> left(nums.begin(), it);
vector<int> right(it+1, nums.end());
root->left = constructMaximumBinaryTree(left);
root->right = constructMaximumBinaryTree(right);
return root;
}
};
The solution above copyies two vectors in each recursion. One way to improve is to use reference instead of copying.
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return makeMBT(nums, 0, nums.size());
}
private:
TreeNode* makeMBT(const vector<int>& nums, int begin, int end) {
if (begin >= end) return nullptr;
auto it = std::max_element(nums.begin()+begin, nums.begin()+end);
TreeNode* root = new TreeNode(*it);
int index = it - nums.begin();
root->left = makeMBT(nums, begin, index);
root->right = makeMBT(nums, index+1, end);
return root;
}
};
145. Binary Tree Postorder Traversal
URL: https://leetcode-cn.com/problems/binary-tree-postorder-traversal/
Description: Given the root of a binary tree, return the postorder traversal of its nodes' values.
(1) Recursive Solution:

class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> ans;
postorderTraversal(root, ans);
return ans;
}
private:
void postorderTraversal(TreeNode* root, vector<int>& ans) {
if (root == nullptr) return;
postorderTraversal(root->left, ans);
postorderTraversal(root->right, ans);
ans.push_back(root->val);
}
};
(2) Iterative Solution:
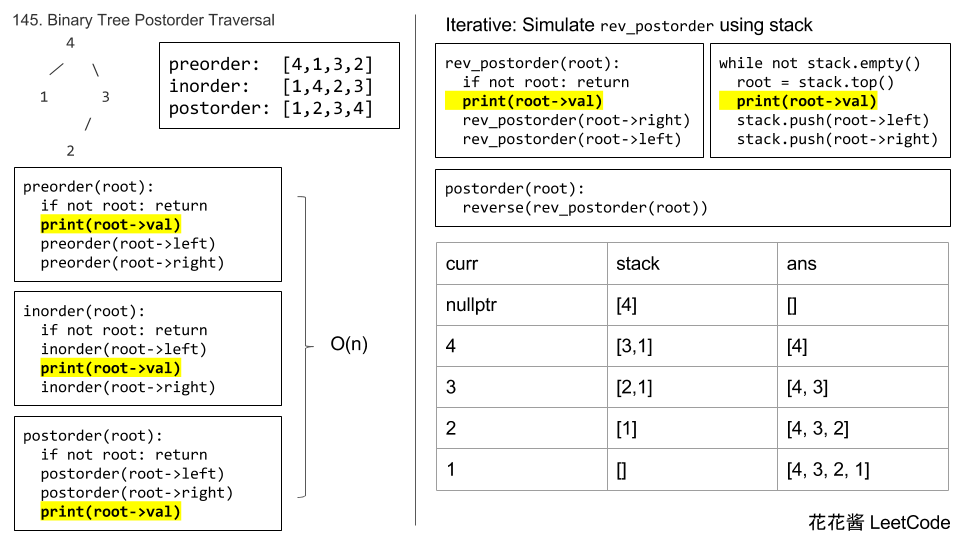
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
if (root == nullptr) return {};
deque<int> ans;
stack<TreeNode*> s;
s.push(root);
while (!s.empty()) {
TreeNode* n = s.top();
s.pop();
// reverse(print(root), traverse(root->right), traverse(root->left))
ans.push_front(n->val);
if (n->left != nullptr) s.push(n->left);
if (n->right != nullptr) s.push(n->right);
}
return vector<int>(ans.begin(), ans.end());
}
};
295. Find Median from Data Stream
URL: https://leetcode-cn.com/problems/find-median-from-data-stream/
Description: Comprehension of median. Then, implement the MedianFinder class.Requirements:
- MedianFinder() initializes the MedianFinder object.
- void addNum(int num) adds the integer num from the data stream to the data structure.
- double findMedian() returns the median of all elements so far.
Constraints:
- -10^5 <= num <= 10^5
- There will be at least one element in the data structure before calling findMedian.
- At most 5 * 10^4 calls will be made to addNum and findMedian.
The first solution: brute force (not accepted)

The second solution: two heap (little tricky)
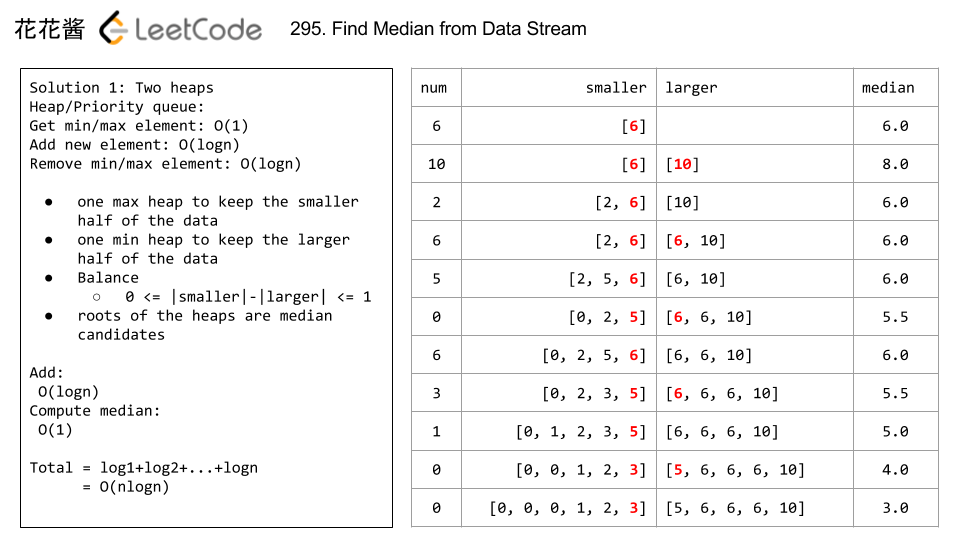
class MedianFinder {
public:
MedianFinder() {}
// Constraints:
// 1. l_.size() >= r_.size()
// 2. l_.size() - r_.size() <= 1
void addNum(int num) {
// Step 1: Add a num into max-heap or min-heap.
if (l_.empty() || num <= l_.top()) {
l_.push(num);
} else {
r_.push(num);
}
// Step 2: Balance max-heap and min-heap.
if (l_.size() < r_.size()) {
l_.push(r_.top());
r_.pop();
} else if (l_.size() - r_.size() == 2) {
r_.push(l_.top());
l_.pop();
}
}
double findMedian() {
if (l_.size() > r_.size()) {
return static_cast<double>(l_.top());
} else {
return (static_cast<double>(l_.top())+static_cast<double>(r_.top())) / 2;
}
}
private:
priority_queue<int, vector<int>, less<int>> l_; // max-heap
priority_queue<int, vector<int>, greater<int>> r_; // min-heap
};
The third solution: balanced binary tree

class MedianFinder {
public:
MedianFinder() {}
void addNum(int num) {
if (m_.empty()) {
l_ = r_ = m_.insert(num);
return;
}
m_.insert(num);
const size_t n = m_.size();
if (n & 1) {
if (num >= *r_) {
l_ = r_;
} else {
l_ = --r_;
}
} else {
if (num >= *r_)
++r_;
else
--l_;
}
}
double findMedian() {
return (static_cast<double>(*l_) + *r_) / 2;
}
private:
multiset<int> m_;
multiset<int>::const_iterator l_;
multiset<int>::const_iterator r_;
};